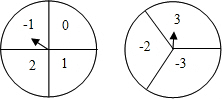
(1)如图所示的转盘中指针落在每个数字上的机会相等,现同时转动A、B两转盘,停止后,指针各指向一个数字.小彬和小颖利用这个转盘做游戏:若两数之积为非负数则小彬胜,否则,-数学
题文
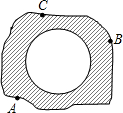
| (1)如图所示的转盘中指针落在每个数字上的机会相等,现同时转动A、B两转盘,停止后,指针各指向一个数字.小彬和小颖利用这个转盘做游戏:若两数之积为非负数则小彬胜,否则,小颖胜.你认为这个游戏对双方公平吗?______(直接写出结果) (2)小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,小明在封闭图形内划出了一个半径为1米的圆,在不远处向圈内掷石子,且记录如下:
  |