题文

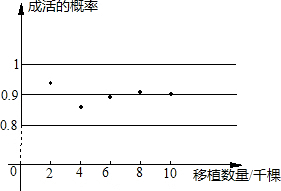
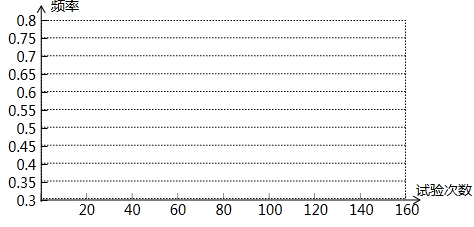
光明中学七（1）班40个同学每10人一组，每人做10次抛掷两枚硬币的实验，想想看“出现两个正面”的频率是否会逐渐稳定下来，得到了下面40个实验结果． 第一组学生学号 101 102 103 104 105 106 107 108 109 110 两个正面成功次数 1 2 3 3 3 3 3 6 3 3 第二组学生学号 111 112 113 114 115 116 117 118 119 120 两个正面成功次数 1 1 3 2 3 4 2 3 3 3 第三组学生学号 121 122 123 124 125 126 127 128 129 130 两个正面成功次数 1 0 3 1 3 3 3 2 2 2 第四组学生学号 131 132 133 134 135 136 137 138 139 140 两个正面成功次数 2 2 1 4 2 4 3 2 3 3 （1）学号为113的同学在他10次实验中，成功了几次？成功率是多少？他是他所在小组同学中成功率最高的人吗？ （2）学号为116和136的两位同学在10次实验中成功率一样吗？如果他们两人再做10次实验，成功率依然会一样吗？ （3）怎么计算每一组学生的集体成功率？哪一组成功率最高？ （4）累计每个学生的实验结果，完成下面的“出现两个正面”的频数、频率随抛掷次数变化统计表，如果把这张表画成相应的图，你会看到什么？ 抛掷次数 50 100 150 200 250 300 350 400 出现两个正面的频数 出现两个正面的频率

题型：解答题  难度：中档

答案

（1）由表格可得出：学号为113的同学在他10次实验中，成功了3次， 成功率是： 3 10 ×100%=30%． 根据该组中116号成功了4次，故他不是他所在小组同学中成功率最高的人． （2）根据学号为116和136的两位同学在10次实验中的成功次数相同， 故学号为116和136的两位同学在10次实验中的成功率是一样的． 如果他们两人再做10次实验，成功率不一定会一样． （3）集体成功率= 小组所有成员实验成功次数总和 小组所有成员实验总次数 ×100%． 第一组成功率：（1+2+3+3+3+3+3+3+6+3）÷（10×10）×100%=30%； 第二组成功率：（1+1+3+2+3+4+2+3+3+3）÷（10×10）×100%=25%； 第三组成功率：（1+0+3+1+3+3+3+2+2+2）÷（10×10）×100%=20%； 第四组成功率：（2+2+1+4+2+4+3+2+3+3）÷（10×10）×100%=26%； 故第一组成功率最高． （4）统计表如下： 抛掷次数 50 100 150 200 250 300 350 400 出现两个正面 的频数 12 30 40 55 63 75 86 101 出现两个正面 的频率 24% 30% 26.7% 27.5% 25.2% 25% 24.6% 25.3% 若绘制成图后，会看到出现两个正面的频率逐渐稳定于25%附近．

据专家权威分析，试题“光明中学七（1）班40个同学每10人一组，每人做10次抛掷两枚硬币的实..”主要考查你对  利用频率估算概率  等考点的理解。关于这些考点的“档案”如下：

利用频率估算概率

考点名称：利用频率估算概率

• 在同样条件下，做大量的重复试验，利用一个随机事件发生的频率逐渐稳定到某个常数，可以估计这个事件发生的概率。
  注：
  （1）当试验的可能结果不是有限个，或各种结果发生的可能性不相等时，一般用统计频率的方法来估计概率；
  （2）利用频率估计概率的数学依据是大数定律：当试验次数很大时，随机事件A出现的频率，稳定地在某个数值P附近摆动.这个稳定值P，叫做随机事件A的概率，并记为P(A)=P。
  （3）利用频率估计出的概率是近似值。