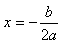题文

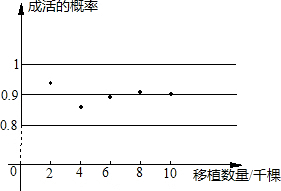
在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只，某学习小组做摸球实验，再把它放回袋中，不断重复，下表是活动进行中的一组统计数据： （1）请估计：当n很大时，摸到白球的频率将会接近多少？ （2）试估算口袋中黑、白两种颜色的球各有多少只？ 摸球的次数 100 150 200 500 800 1000 摸到白球的次数 58 96 116 295 484 601 摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601

题型：解答题  难度：中档

答案

（1）由图表可知当n很大时，摸到白球的频率将会接近0.6， 因为当n≥500，频率值稳定在0.6左右， 由此，当n很大时，摸到白球的频率将会接近0.6； （2）白球个数：20×0.6=12只， 黑球个数：20×0.4=8只．

据专家权威分析，试题“在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20..”主要考查你对  利用频率估算概率，二次函数的最大值和最小值  等考点的理解。关于这些考点的“档案”如下：

利用频率估算概率二次函数的最大值和最小值

考点名称：利用频率估算概率

• 在同样条件下，做大量的重复试验，利用一个随机事件发生的频率逐渐稳定到某个常数，可以估计这个事件发生的概率。
  注：
  （1）当试验的可能结果不是有限个，或各种结果发生的可能性不相等时，一般用统计频率的方法来估计概率；
  （2）利用频率估计概率的数学依据是大数定律：当试验次数很大时，随机事件A出现的频率，稳定地在某个数值P附近摆动.这个稳定值P，叫做随机事件A的概率，并记为P(A)=P。
  （3）利用频率估计出的概率是近似值。

考点名称：二次函数的最大值和最小值

• 二次函数的最值：
  1.如果自变量的取值范围是全体实数，则当a>0时，抛物线开口向上，有最低点，那么函数在处取得最小值y_最小值=；
  当a<0时，抛物线开口向下，有最高点，即当时，函数取得最大值，y_最大值=。
  也即是：如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当时，。
  2.如果自变量的取值范围是，那么，首先要看是否在自变量取值范围内，若在此范围内，则当x=时，；若不在此范围内，则需要考虑函数在范围内的增减性，如果在此范围内，y随x的增大而增大，则当x=x₂ 时，，当x=x₁ 时；如果在此范围内，y随x的增大而减小，则当x=x₁时，，当x=x₂时 。