濠殿喗锚閻°劌危閹间焦鍎戦柛蹇曞帶閻ㄧ偓淇婇锝勬倣缂佽鲸绻勬禒锔芥綇閵娤€锕傛煟椤忓嫷妲搁柛銏$叀閹虫洖顫濋妷銏犱壕闁稿本渚楅崕姗€姊婚崒銈呮灕妞ゃ垺鍨剁粋宥夊传閸曨偆顔岄梻渚囧弿缂嶁偓缂佹梻鍠栭弫宥夋偄閻戞ḿ鐣抽梺娲讳海閸嬫劕鈻旈埡鍛剮闁割偅绻嶅Σ閬嶆煏閸℃鈧鏅堕悩铏弿閻庯綆鍠掗崑鎾存媴鐟欏嫅姘辨喐閻楀牆閲滅紒杈ㄧ箞瀹曪綁宕奸妷銏犱壕濞达絽鎲¢崑妯兼喐閻楀牆绗掓鐐存崌婵℃挳宕掑┑鍡╀户闂佸憡甯炴晶妤呮儓濞嗘挸纭€婵°倕瀚崹浣糕槈閹剧鏀绘俊宸墴閺佸秶浠﹂挊澶岋紟婵炴垶鎸稿ú銈夊箯娴兼潙鍙婇柕澶堝€楃粔鍫曟煏閸☆厽瀚�
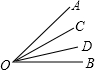
如图,∠AOB=130°,射线OC是∠AOB内部任意一条射线,OD、OE分别是∠AOC、∠BOC的平分线,下列叙述正确的是()A.∠DOE的度数不能确定B.∠AOD+∠BOE=∠EOC+∠COD=∠DOE=65°C.∠BOE=2∠CODD.-数学
题文
如图,∠AOB=130°,射线OC是∠AOB内部任意一条射线,OD、OE分别是∠AOC、∠BOC的平分线,下列叙述正确的是( )
 |
答案
| ∵OD、OE分别是∠AOC、∠BOC的平分线, ∴∠AOD=∠COD、∠EOC=∠BOE, 又∵∠AOD+∠BOE+∠EOC+∠COD=∠AOB=130°, ∴∠AOD+∠BOE=∠EOC+∠COD=∠DOE=65°. 故选B. |
据专家权威分析,试题“如图,∠AOB=130°,射线OC是∠AOB内部任意一条射线,OD、OE分别是∠..”主要考查你对 角平分线的定义 等考点的理解。关于这些考点的“档案”如下:
角平分线的定义
考点名称:角平分线的定义
- 角的平分线的定义:
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。 角平分线的性质:
角平分线上的点,到角两边的距离相等
定理:
角平分线上的任意一点,到角两边的距离相等。垂直于两边为最短距离。角平分线能得到相同的两个角。三角形三条角平分线相交于一点,并且这一点到三边的距离相等。
逆定理:
到角两边的距离相等的点在角平分线上。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数;(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.-数学
下一篇:如图,∠AOC=90°,ON是锐角∠COD的角平分线,OM是∠AOD的角平分线,那么,∠MON=()A.12∠COD+45°B.90°C.12∠AODD.45°-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |