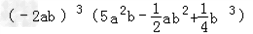若n0=a0+b0,则可产生新数n1=a0b0,若n1=a1+b1,则可产生新数n2=a1b1,若n2=a2+b2,则可产生新数n3=a2b2;….按此方法可产生一系列新数:n1,n2,n3….问能否用这种方法数次,由-数学
题文
| 若n0=a0+b0,则可产生新数n1=a0b0, 若n1=a1+b1,则可产生新数n2=a1b1, 若n2=a2+b2,则可产生新数n3=a2b2;…. 按此方法可产生一系列新数:n1,n2,n3….问能否用这种方法数次,由数10逐步产生数2003,若能,请写出一个产生的过程;若不能,请说明理由. |


![化简-(-2a+4b-c)的结果为[]A.2a+4b-cB.2a-4b-cC.2a-4b+cD.-2a+4b-c-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/77/2019-04-06/f85462bbc3efb07bd59e9b75839bd034.png)