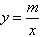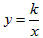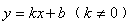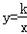题文

如图，点M是反比例函数y= 1 x 在第一象限内图象上的点，作MB⊥x轴于B．过点M的第一条直线交y轴于点A1，交反比例函数图象于点C1，且A1C1= 1 2 A1M，△A1C1B的面积记为S1；过点M的第二条直线交y轴于点A2，交反比例函数图象于点C2，且A2C2= 1 4 A2M，△A2C2B的面积记为S2；过点M的第三条直线交y轴于点A3，交反比例函数图象于点C3，且A3C3= 1 8 A3M，△A3C3B的面积记为S3；以此类推…；则S1+S2+S3+…+S8=______．

题型：填空题  难度：偏易

答案

过点M作MD⊥y轴于点D，过点A1作A1E⊥BM于点E，过点C1作C1F⊥BM于点F， ∵点M是反比例函数y= 1 x 在第一象限内图象上的点， ∴OB×BM=1， ∴S△A1BM= 1 2 OB×MB= 1 2 ， ∵A1C1= 1 2 A1M，即C1为A1M中点， ∴C1到BM的距离C1F为A1到BM的距离A1E的一半， ∴S1=S△BMC1= 1 2 S△A1BM= 1 4 ， ∴S△BMA2= 1 2 BM?A2到BM距离= 1 2 ×BM×BO= 1 2 ， ∵A2C2= 1 4 A2M， ∴C2到BM的距离为A2到BM的距离的 3 4 ， ∴S2=S△A2C2B= 1 4 S△BMA2= 1 8 ， 同理可得：S3= 1 16 ，S4= 1 32 … ∴ 1 4 + 1 8 +…+ 1 28 + 1 29 ， = 1 4 + 1 8 +…+ 1 256 + 1 512 ， = 255 512 ， 故答案为： 255 512 ．

据专家权威分析，试题“如图，点M是反比例函数y=1x在第一象限内图象上的点，作MB⊥x轴于B..”主要考查你对  求反比例函数的解析式及反比例函数的应用  等考点的理解。关于这些考点的“档案”如下：

求反比例函数的解析式及反比例函数的应用

考点名称：求反比例函数的解析式及反比例函数的应用

• 反比例函数解析式的确定方法：
  由于在反比例函数关系式 ：y= 中，只有一个待定系数k，确定了k的值，也就确定了反比例函数。因此，只需给出一组x、y的对应值或图象上一点的坐标，代入中即可求出k的值，从而确定反比例函数的关系式。但在实际求反比例函数的解析式时，应该具体问题具体分析。

  反比例函数的应用：
  建立函数模型，解决实际问题。

• 用待定系数法求反比例函数关系式的一般步骤是：
  ①设所求的反比例函数为：y= (k≠0)；
  ②根据已知条件（自变量与函数的对应值）列出含k的方程；
  ③由代人法解待定系数k的值；
  ④把k值代人函数关系式y= 中。
  
  反比例函数应用一般步骤：
  ①审题；
  ②求出反比例函数的关系式；
  ③求出问题的答案，作答。